How Does Private Payment Work?

Manta is all about bringing privacy to the wider blockchain space, and an important part of making privacy practical to use is the construction of simple and powerful privacy primitives. The first and most powerful primitive we are building is Private Payment, more specifcally, a multi-asset decentralized anonymous payment protocol.

How Does It Work?

We recently posted a tech talk that explains the protocol in some detail:

You can follow along with this video, download the slides, and/or keep reading below to get an overview and some technical details about how Private Payment works.

Currently, the formal specification for Private Payment is still closed source, but stay tuned for its public release in the near future!

Public Ledgers

Most decentralized systems of digital money use what are called public ledgers to keep track of the flow of money. Public ledgers store the current state of every participant's balances, and whenever someone tries to spend from their account, the blockchain will come to consensus on whether this transaction is valid and updates the state. However, to validate a transaction the public ledger needs to know which sender and receiver are participating, and what amount is being transfered. We would like to find a way to avoid this and preserve the privacy of all parties involved in transactions and keep amounts private as well.

Properties of a Decentralized Anonymous Payment Protocol

When designing a private ledger, we want the following two properties to hold:

1. A transaction cannot modify the total supply of an asset. Only the ownership, the exclusive right to spend the asset in the future, can change.
2. Reading the ledger cannot reveal any information about a transaction or existing user balances

These two properties seem to be at odds with each other since we want to verify that the total supply remains fixed but we must do so without learning what the underlying transaction is!

Fortunately, some new cryptographic protocols can save the day, namely zkSNARKs, zero-knowledge Succinct Non-interactive ARguments of Knowledge. We will see later which role they play in privatizing the payment protocol.

Overview

We will first describe a simplified version of the protocol, following two imaginary participants Alice and Bob, and we want to find a way to have Alice send an asset to Bob using a private Ledger. We will describe the protocol in the following steps:

1. Send and Receive
2. Shared Secrets
3. Encrypt and Decrypt
4. Ownership Certificates
5. Zero-Knowledge Transfer Proof

This discussion is not entirely self-contained but we will attempt to explain cryptographic protocols only as black boxes by their interfaces and security guarantees. Further reading on each of the subjects below is encouraged.

Participants (in detail)

• Alice (sender): a participant that already has access to some assets and is guaranteed by the Ledger the ability to spen them.
• Bob (receiver): a participant that can be uniquely identified by other senders and will be guaranteed the ability to spend received assets in the future.
• Ledger: represents all public information (the state) and the network of validators (blockchain) which come to consensus on the private transfer of ownership of assets between senders and receivers.

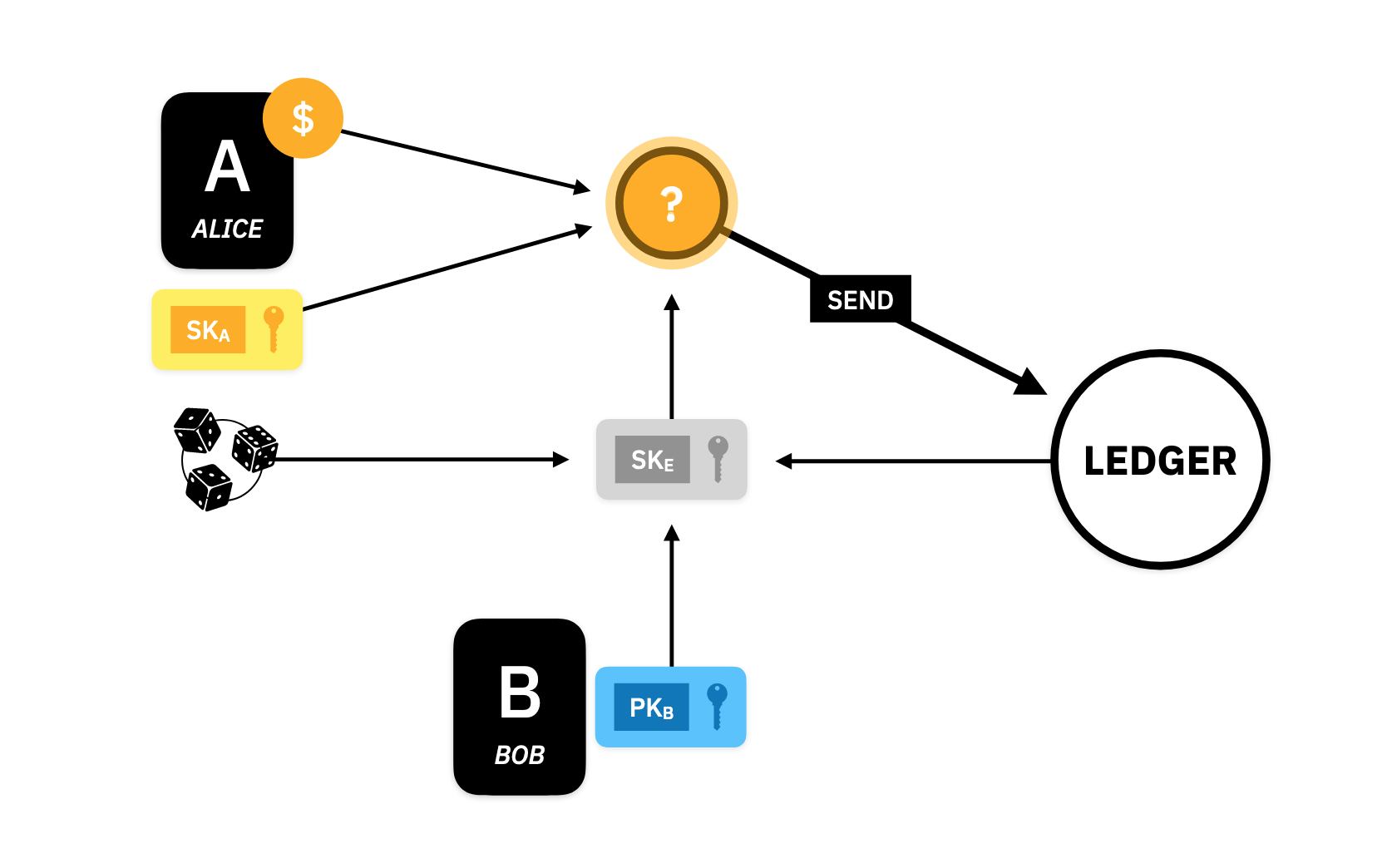
Send and Receive

For Alice to send her assets to Bob, she communicates with the Ledger as an intermediary. The Ledger operates asynchronously and is distributed across the internet, and so, many computers can access the Ledger and send and receive messages to and from the network. Alice will send a transfer message to the Ledger and if accepted, it will be used to update the state of the Ledger, and the changes are propagated to all of the network. Bob will query the network, asking for new updates to the state. If there is a new Ledger state, he will download it and analyze it to see if he has received any new assets. Here are those two protocols in detail:

Send

Alice begins by constructing a special number called $\textsf{SK}_\textsf{E}$, the ephemeral secret key, which she will use to represent this unique transfer. She constructs it by taking Bob's pubic key, $\textsf{PK}_\textsf{B}$, some public data from the Ledger, and some randomness:

This is built using a commitment scheme which commits to $\Lambda$ (the ledger checkpoint), and $\textsf{PK}_\textsf{B}$ using $\tau$ as the randomness (A.K.A blinder, or trapdoor):

$$\textsf{SK}_\textsf{E} := \textsf{COM}(\Lambda || \textsf{PK}_\textsf{B}, \tau)$$

This ephemeral key is only used once. Alice will have to prove later that she constructed $\textsf{SK}_\textsf{E}$ properly, called opening the commitment. The commitment is binding which means that Alice will not be able to change her mind and find another public key or ledger checkpoint to construct the same ephemeral key. The trapdoor $\tau$ gives us the hiding property which means that even if someone knows $\Lambda$ and $\textsf{PK}_\textsf{B}$ they won't be able to predict what $\textsf{SK}_\textsf{E}$ is without knowing $\tau$.

Alice now uses the ephemeral key, $\textsf{SK}_\textsf{E}$, her own secret key $\textsf{SK}_\textsf{A}$, and the asset that she received from the Ledger earlier, to build a private asset. We will see as we go along how exactly the private asset is built.

Receive

Once Alice finishes her communication with the Ledger and the Ledger accepts her private asset, it will store that private asset forever, waiting for someone to claim it. Bob wishes to claim it, so he goes to the Ledger and asks for all of the newest private assets since his last query. The Ledger will send them to Bob and he will use his secret key $\textsf{SK}_\textsf{B}$ to scan through the private assets to find the ones he now owns.

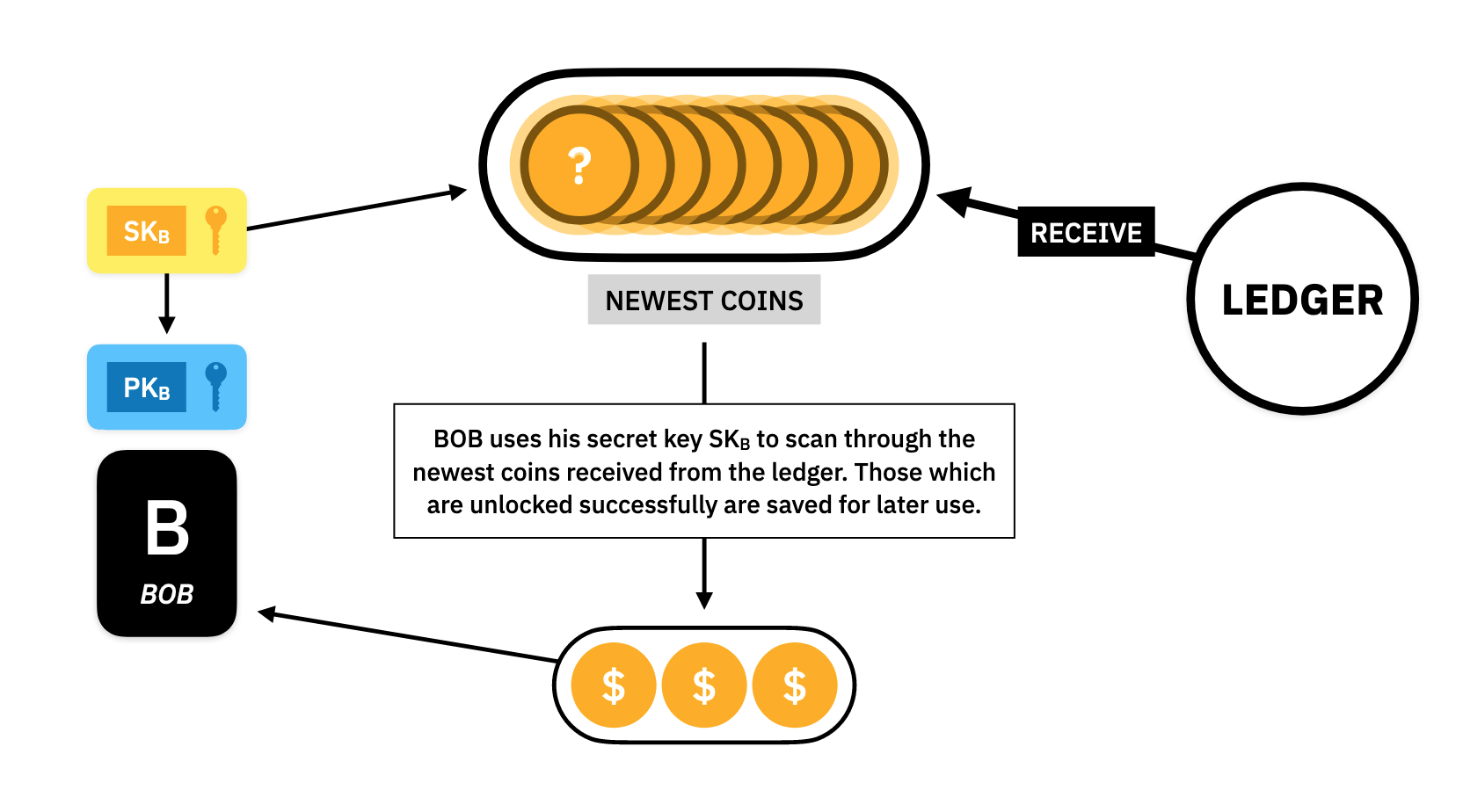
The secret key that Bob is using for this scanning process must be the one that derived the public key $\textsf{PK}_\textsf{B}$ which Alice used to build the private asset. This key derivation must be irreversible so that no one can discover (in a reasonable amount of time) what $\textsf{SK}_\textsf{B}$ is just from the knowledge of $\textsf{PK}_\textsf{B}$.

NOTE: Because the Ledger will be around for a long time, Bob can wait as long as he likes to receive the new private assets.

Shared Secrets

But how will Bob be able to claim is new assets? How will he be able to spend them in the future?

One of the most important cryptographic tools that we can take advantage of here is the shared secret. Essentially, we want to find a way to take some information and wrap it up so that only two people have access to it. Getting someone to share a secret with themselves is easy, they just don't tell anyone. But how do we tell someone else our secrets so that only the two of you ever know what it is?

One of the most common ways to do this is with the Diffie-Hellman Key Exchange protocol. In this protocol, we take an operation that we assume is impossible to reverse (in a reasonable amount of time), let's call it $\textsf{bind}$, and a public constant $G$ that everyone agrees on. We choose $\textsf{bind}$ and $G$ so that it has the following property:

$$\textsf{bind}(y, \textsf{bind}(x, G)) = \textsf{bind}(x, \textsf{bind}(y, G))$$

Let's call $x$ and $y$ secret keys and call $X := \textsf{bind}(x, G)$ and $Y := \textsf{bind}(y, G)$ public keys. Since $\textsf{bind}$ is irreversible, we can leave $X$ and $Y$ out in the open for anyone to see, or even if we want to be discrete we can still send $X$ or $Y$ to only a particular person, but we don't have to worry that someone can reverse engineer our keys if they get their hands on it.

Because the $\textsf{bind}$ function has the property above, we actually have our shared secret:

$$S := \textsf{bind}(y, X) = \textsf{bind}(x, Y)$$

So if you share your public key $X$ with someone and get their public key $Y$, then you both can compute the shared secret, $S$. In the rest of the protocol, Alice and Bob will share several secrets on their way to performing a successful transfer.

Encrypt and Decrypt

The first place that Alice and Bob use shared secrets is to share encryption keys. These keys are used to send the asset value that we want to transfer in a secret message from Alice to Bob. This is called the in-band secret distribution.

Encryption

For Alice to send the asset value to Bob, she uses a hybrid public-key encryption scheme to encrypt the asset. She does this by taking Bob's public key $\textsf{PK}_\textsf{B}$ and the ephemeral secret key for this particular transaction $\textsf{SK}_\textsf{E}$ and performing a Diffie-Hellman Key Exchange (in this case using elliptic curves to define the $\textsf{bind}$ function), to compute a shared encryption key $K$.

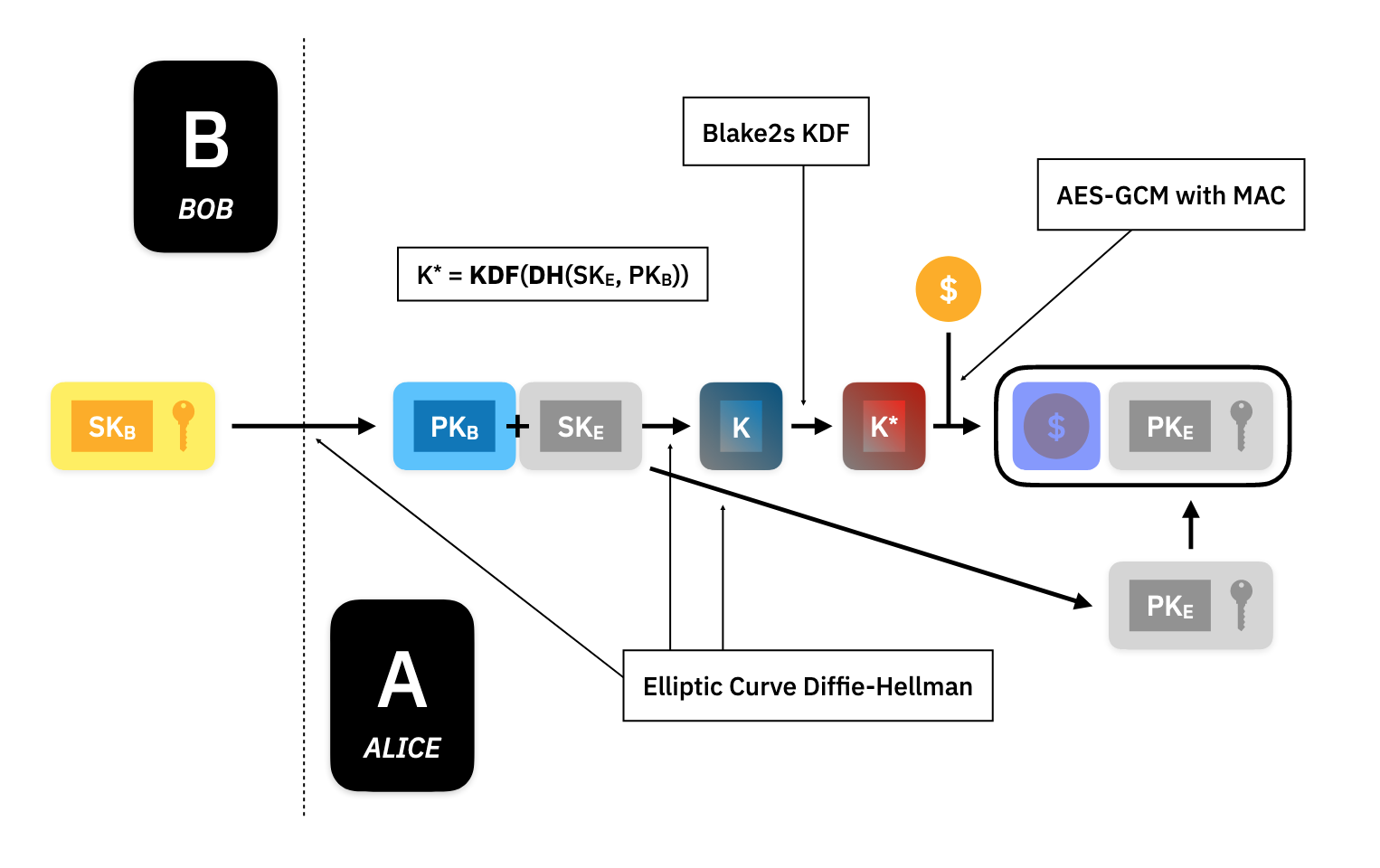
Alice then uses the Blake2s key derivation function to produce another key $K^*$ which will be the right size for the standard AES-GCM encryption scheme with message authentication. Alice encrypts the asset with $K^*$ and appends the derived public ephemeral key $\textsf{PK}_\textsf{E}$ to the ciphertext message. This forms part of the private asset that Alice sends to the Ledger.

Decryption

Bob will then download the new private assets from the Ledger, and to see if any of the new assets are his to spend, he will try to decrypt them by building the same shared secrets Alice used for encryption.

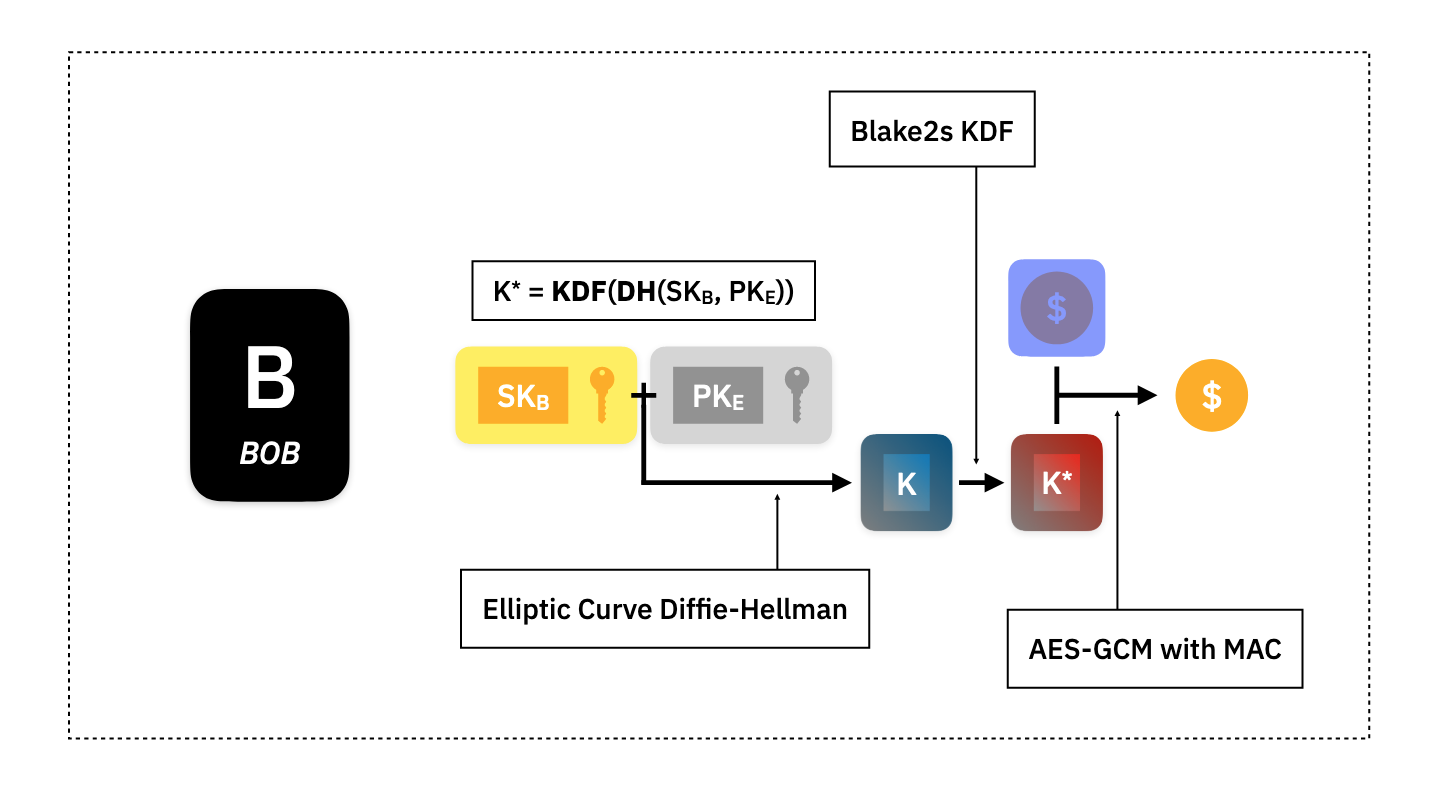
In this case, Bob uses his secret key, $\textsf{SK}_\textsf{B}$, and the public ephemeral key attached to the private asset, $\textsf{PK}_\textsf{E}$, to build the Diffie-Hellman shared secret, $K$, then using the same Blake2s function to derive $K^*$, and then performing AES-GCM decryption. The decryption will check that the message authentication can be reconstructed properly and if the key $K^*$ was different than the one used to build the message, it will fail, and Bob will know the asset is not his. If the encryption succeeded, then Bob will store the private asset on his local computer to spend later.

Ownership Certificates

Now we know how Alice can communicate to Bob the amount of value she has sent to him. But still, the Ledger must only accept asset transfers which can provably transfer the future spending power from the sender to the receiver, all the while, preserving the privacy of all parties involved. Just because Alice sends Bob an encrypted asset does not mean she cannot send it again, or send it to someone else. We need a way to keep track of who owns what and be able to take away that power once someone spends an asset.

To satisfy this constraint, Alice will generate two kinds of certificates, UTXOs and void numbers.

A UTXO or Unspent Transation Output, is a certificate for the future spending of one of the receivers of a transaction. It is used in some public ledger protocols in the following way:

1. Prove that Alice owns one of the current UTXOs
2. Drop Alice's UTXO from the Ledger
3. Create a new UTXO for Bob

In this way, the current set of UTXOs represents all of the users which have some amount of assets and how much they all own. For Alice to spend her asset, she needs to present a certificate $\textsf{CM}_\textsf{A}$ which represents that Alice was a receiver in a past transaction. She will need to prove that the Ledger has seen this UTXO before.

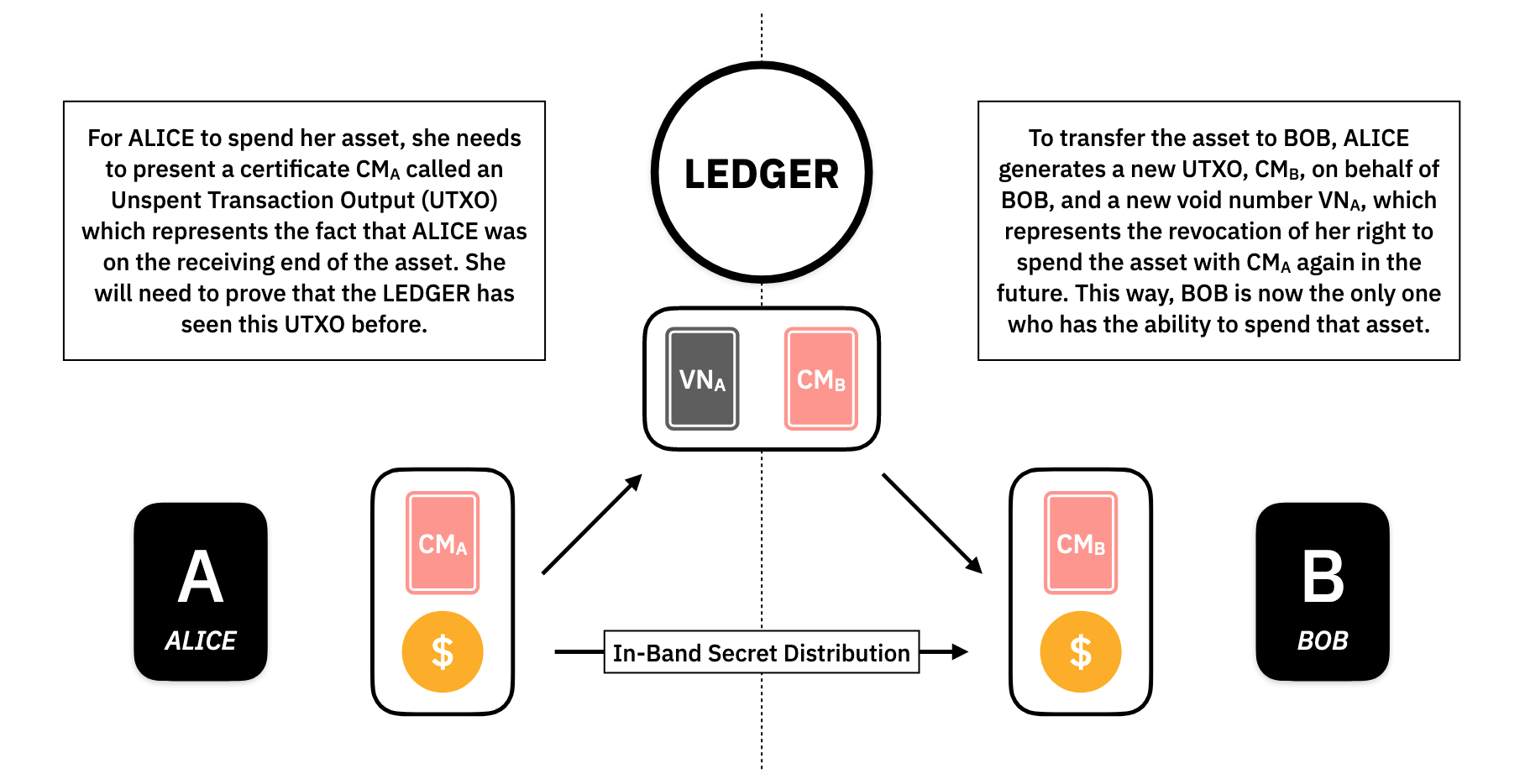
To transfer the asset to Bob, Alice generates a new UTXO, called $\textsf{CM}_\textsf{B}$, on Bob's behalf. Alice will also need to revoke her old UTXO somehow. She does this by generating a void number, $\textsf{VN}_\textsf{A}$, which is tied to her $\textsf{CM}_\textsf{A}$ in such a way that:

1. The same $\textsf{CM}_\textsf{A}$ will always generate the same $\textsf{VN}_\textsf{A}$.
2. Different $\textsf{CM}$ generate different $\textsf{VN}$.
3. No one can tell which $\textsf{CM}_\textsf{A}$ the $\textsf{VN}_\textsf{A}$ belongs to.
4. Only Alice can construct $\textsf{VN}_\textsf{A}$.

Let's see how $\textsf{CM}$ and $\textsf{VN}$ are constructed.

Receiver Certificates

In order for Alice to create $\textsf{CM}_\textsf{B}$ on Bob's behalf, she computes another shared secret, called $\textsf{T}_\textsf{B}$, the trapdoor, to the UTXO commitment $\textsf{CM}_\textsf{B}$.

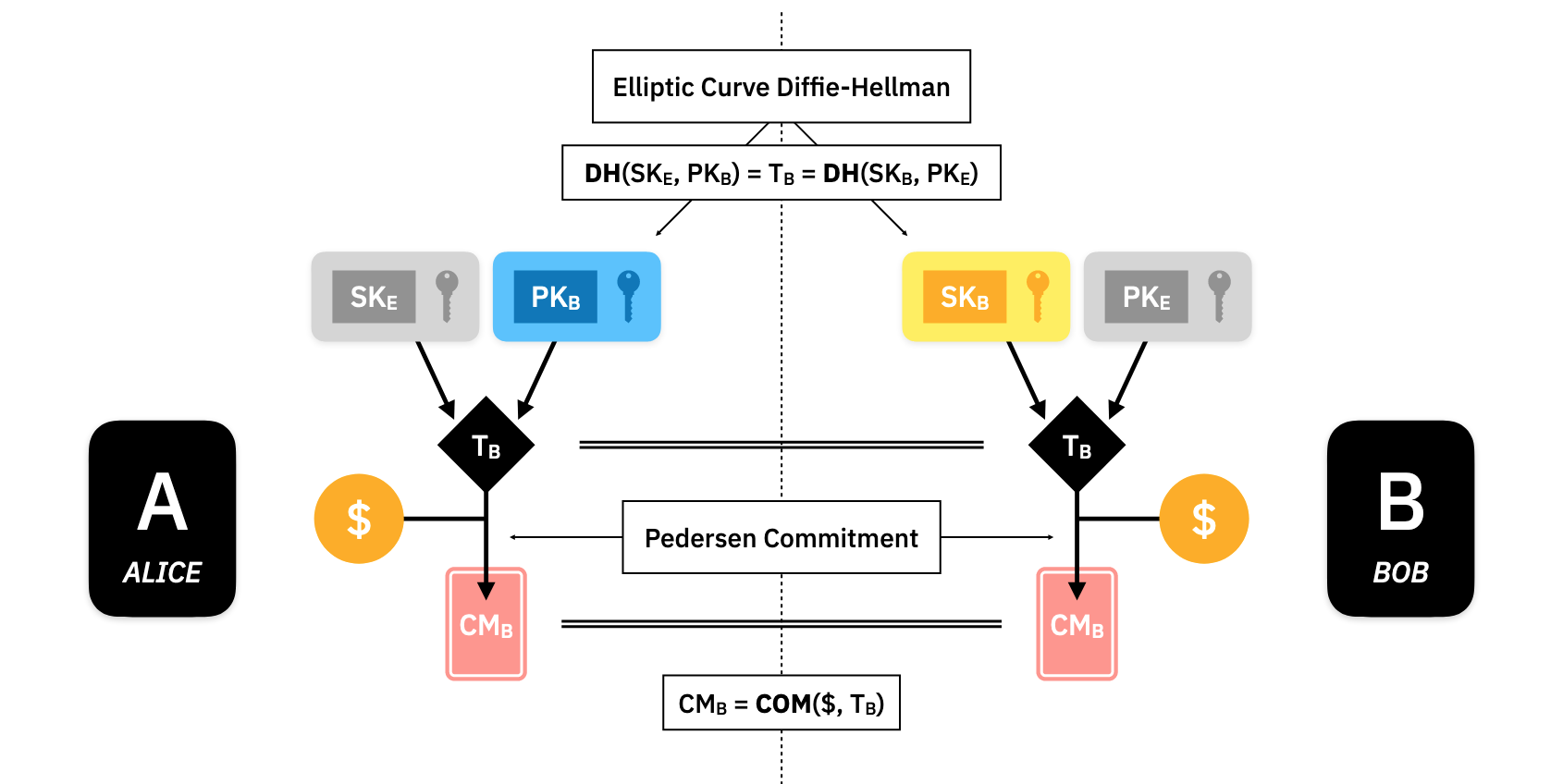
The commitment consists of the asset amount that Alice wants to transfer and the shared trapdoor. The trapdoor is the random part of the commitment that ensures the hiding property. The binding property of the commitment ensures that Alice can't put some fake information into the commitment and then Bob ends up with some assets he can't spend.

Sender Certificates

For Alice to generate her void number certificate, she takes the trapdoor, $\textsf{T}_\textsf{A}$ that was used to build her $\textsf{CM}_\textsf{A}$, and commits to her secret key $\textsf{SK}_\textsf{A}$.

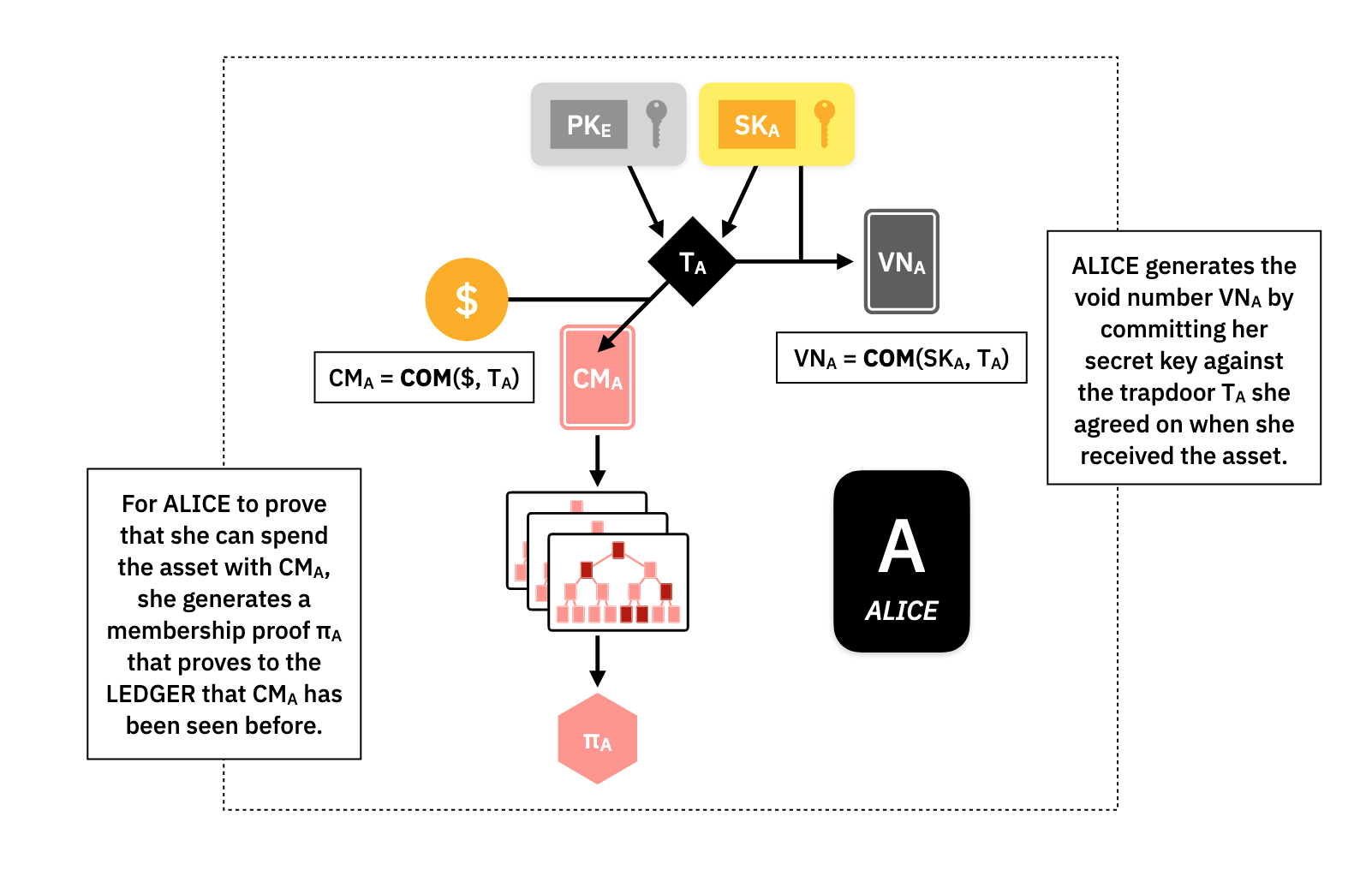
The void number $\textsf{VN}_\textsf{A}$ is tied to the commitment because it uses the same trapdoor, and only Alice can perform this computation because $\textsf{SK}_\textsf{A}$ is only known to her.

In order to prove that her UTXO is already on the Ledger, Alice can create a Merkle-Proof, $\pi_\textsf{A}$, attesting to this fact.

Zero-Knowledge Transfer Proof

But Alice has done all of these computations in secret, involving a lot of secret information which would compromise her account if she shared with anyone. How can the Ledger trust that she did this computation fairly?

Alice can take advantage of zkSNARKs, zero-knowledge Succinct Non-interactive Arguments of Knowledge to do the computation entirely on her own machine. zkSNARKs work like this:

1. Alice and the Ledger agree in public on some algorithm to check (ex: some computer program to execute or the protocol above). They agree on which variables in the algorithm are secret and which are public.
2. Alice performs the computation of that algorithm on her own machine with her own chosen secret input and public input.
3. Using the output of the computation, Alice builds a proof $\pi$ that the computation was done correctly (because of succinctness, this is a very small file compared to the size of the algorithm)
4. Alice sends $\pi$ to the Ledger and it can check quickly if the computation that produced this file was in-fact the agreed-upon algorithm in which case he accepts or rejects.

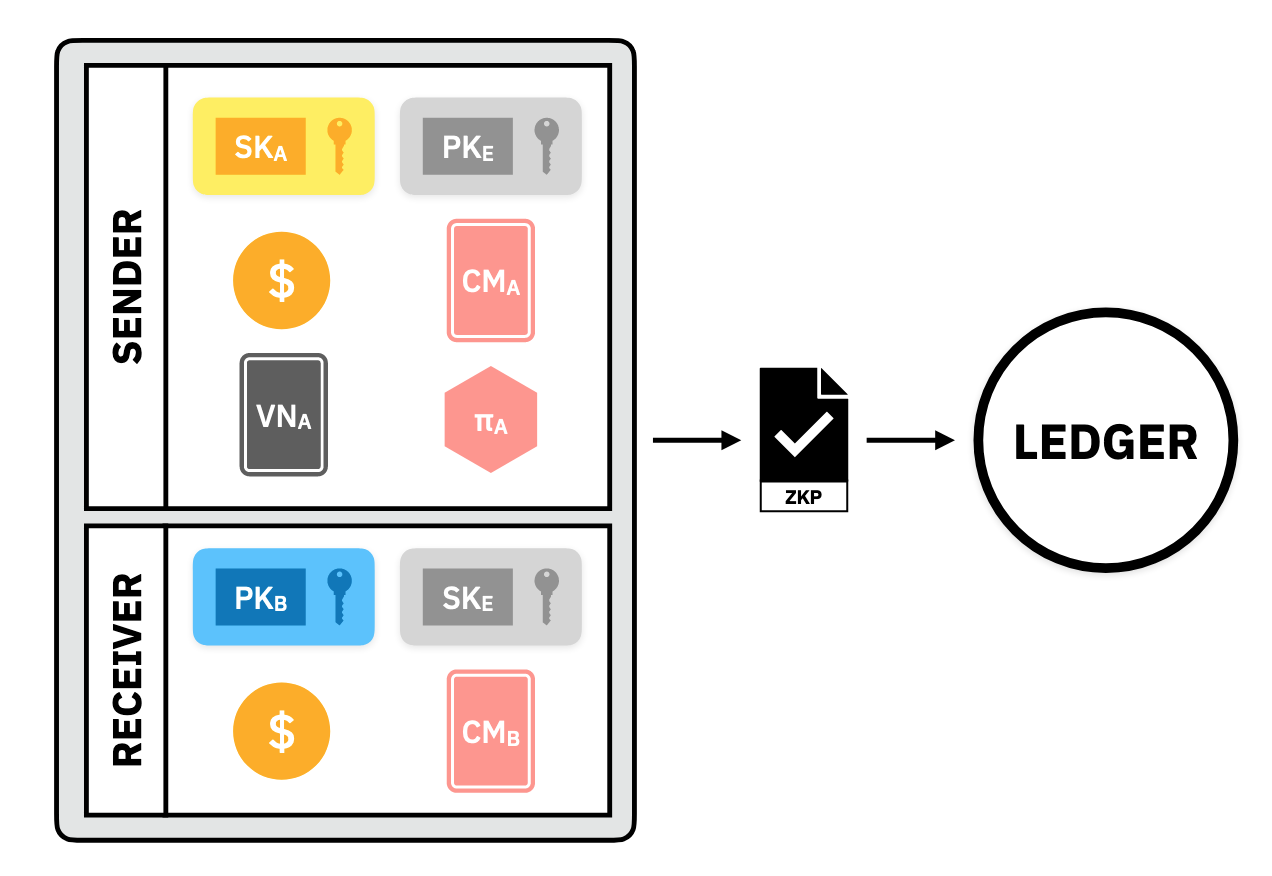
Alice can use zkSNARKs to compute all the different objects in the Private Payment Protocol above. When she does this, she gains the following privacy guarantees:

1. Private Sender: Because $\textsf{CM}_\textsf{A}$ and $\pi_\textsf{A}$ are secret, the Ledger won't know which UTXO belongs to Alice, just that it is in fact one of the ones stored on the Ledger.
2. Private Receiver: Because the construction of $\textsf{SK}_\textsf{E}$ is secret, no one knows that it comes from $\textsf{PK}_\textsf{B}$.
3. Private Asset: Because $\textsf{SK}_\textsf{E}$, $\textsf{PK}_\textsf{B}$, and the asset amount are secret, no one can decrypt the encrypted asset except Bob.

So we have successfully built a Private Payment Protocol!

Generalized N-to-M Transfer Protocol

In general, we need more than just a 1-to-1 transfer to be able to have usable money. For example, if Alice sends Bob five units and he wants to send Carol three units, he cannot use a 1-to-1 because he can't subdivide his assets. To do this, we generalize the above protocol to an $N$-to-$M$ protocol.

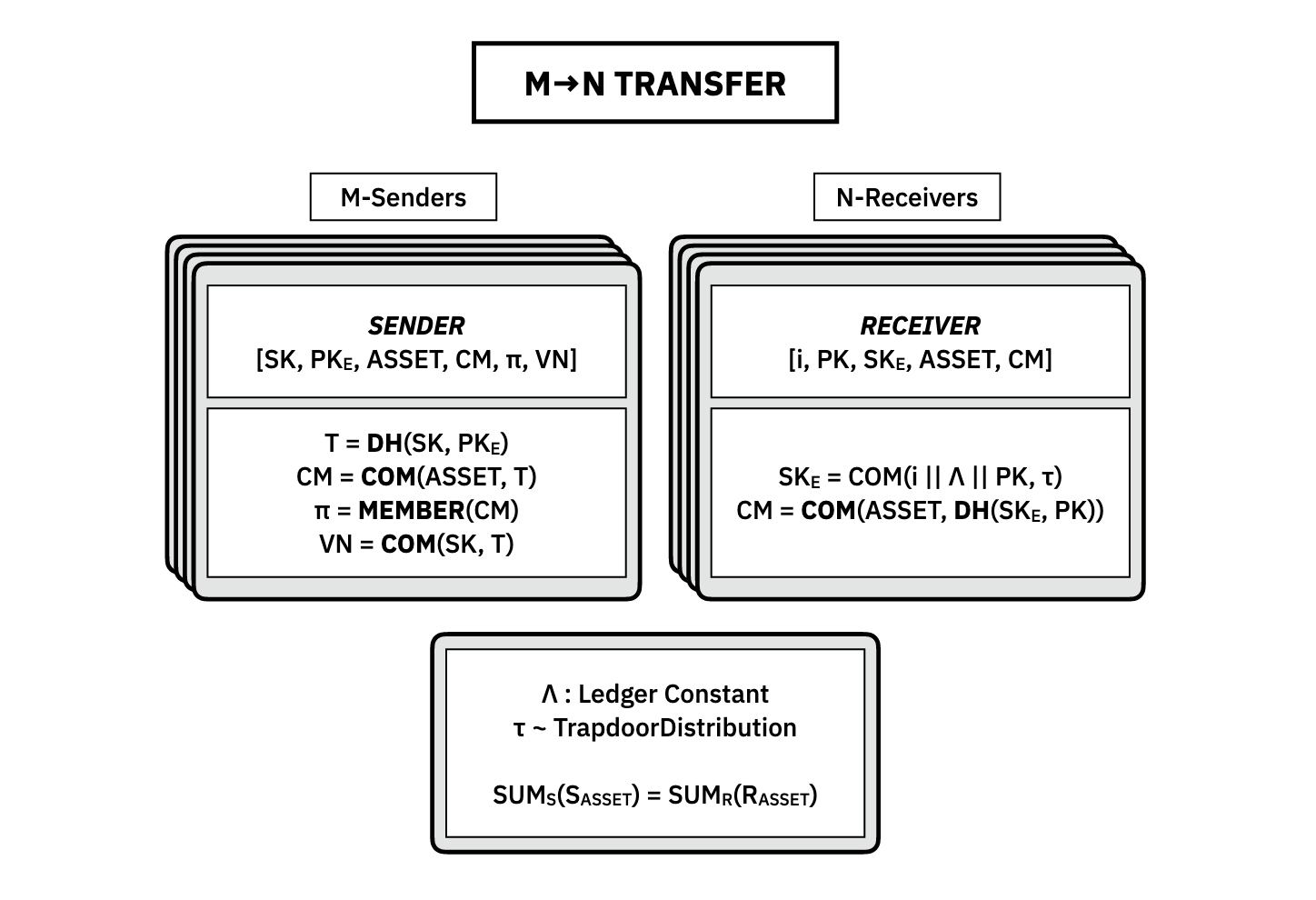
We can repeat the construction for each individual sender and receiver and so Bob can send his asset to Carol by sending three units to her and sending two back to himself. Because the entire protocol is private, no one except Bob knows that he has done this.

There's More

There are some more details that you have to get right to build a real Private Payment scheme, like private wallets, fee proxies, and more. Right now these ideas are still brewing, but there's some cool stuff coming soon, so stay tuned!